
The basic structure of the new ReiserFS—graphs vs. trees, keys, nodes and blocks.
One way of organizing information is to put it into trees. When we organize information in a computer, we typically sort it into piles called nodes, with a name (pointer) for each pile. Some of the nodes contain pointers, and we can look through the nodes to find those pointers to (usually other) nodes.
We are interested particularly in how to organize so we actually can find things when we search for them. A tree is an organizational structure that has some useful properties for that purpose. We define a tree as follows:
A tree is a set of nodes organized into a root node and zero or more additional sets of nodes, called subtrees.
Each of the subtrees is a tree.
No node in the tree points to the root node, and exactly one pointer from a node in the tree points to each non-root node in the tree.
The root node has a pointer to each of its subtrees, that is, a pointer to the root node of the subtree.
Note that a single node with no pointers is a tree, because it is the root node. Also, a tree can be a linear tree of nodes without branches.
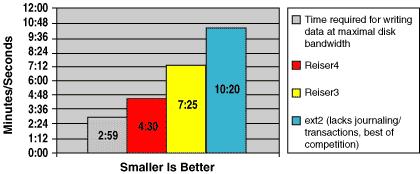
Figure 1. Write Performance (30 Copies Linux Kernel 2.4.18)
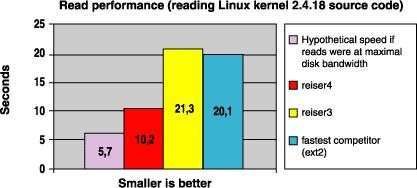
Figure 2. Read Performance (Reading Linux Kernel 2.4.18 Source Code)
It is interesting to argue about whether finite should be a part of the definition of trees. There are many ways of defining trees, and which is the best definition depends on your purpose. Professor Donald Knuth supplies several definitions of tree. As his primary definition of tree he even supplies one which has no pointers, edges or lines in the definition, only sets of nodes.
Knuth defines trees as being finite sets of nodes. There are papers on inifinte trees on the Internet. I think it more appropriate to consider finite an additional qualifier on trees, rather than bundling finite into the definition. However, I personally only deal with finite trees in my research.
Edge is a term often used in tree definitions. A pointer is unidirectional, meaning you can follow it from the node that has it to the node it points to, but you cannot follow it back from the node it points to, to the node that has it. An edge, however, is bidirectional, meaning you can follow it in both directions.
Here are three alternative tree definitions, which are interesting in how they are mathematically equivalent to each other. They are not equivalent to the definition I supplied, because edges are not equivalent to pointers. For all three of these definitions, let there be no more than one edge connecting the same two nodes:
a set of vertices (aka points) connected by edges (aka lines) for which the number of edges is one less than the number of vertices;
a set of vertices connected by edges that have no cycles (a cycle is a path from a vertex to itself);
or a set of vertices connected by edges for which there is exactly one path connecting any two vertices.
These three alternative definitions do not have a unique root in their tree, and such trees are called free trees.
The definition I supplied is a definition of a rooted tree, not a free tree. It also has no cycles, it has one less pointer than it has nodes, and there is exactly one path from the root to any node.
Consider the purposes for which you might want to use a graph and those for which you might want to use a tree. In a tree there is exactly one path from the root to each node in the tree, and a tree has the minimum number of pointers sufficient to connect all the nodes. This makes it a simple and efficient structure. Trees are useful when efficiency with minimal complexity is desired and when there is no need to reach a node by more than one route.
Reiser4 has both graphs and trees, with trees used when the filesystem chooses the organization (in what we call the storage layer, which tries to be simple and efficient) and graphs when the user chooses the organization (in the semantic layer, which tries to be expressive so that the user can do whatever he or she wants).
We assign a key to everything stored in the tree. We find things by their keys, and using them gives us additional flexibility in how we sort things. If the keys are small, we have a compact means of specifying enough information to find the thing. It also limits what information we can use for finding things.
This limit restricts the key's usefulness, and so we have a storage layer, which finds things by keys, and a semantic layer, which has a rich naming system (described in Part II of this article). The storage layer chooses keys for things solely to organize storage in a way that improves performance, and the semantic layer understands names that have meaning to users. As you read, you might want to think about whether this is a useful separation that allows the freedom to add improvements that aid performance in the storage layer, while escaping paying a price for the side effects of those improvements on the flexible naming objectives of the semantic layer.
We start our search at the root, because from the root we can reach every other node. But, how do we choose which subtree of the root to go to from the root? The root contains pointers to its subtrees. For each pointer to a subtree there is a corresponding left delimiting key. Pointers to subtrees, and the subtrees themselves, are ordered by their left delimiting key. A subtree pointer's left delimiting key is equal to the least key of the things in the subtree. Its right delimiting key is larger than the largest key in the subtree, and it is the left delimiting key of the next subtree of this node.
Each subtree contains only things whose keys are at least equal to the left delimiting key of its pointer and are not more than its right delimiting key. If there are no duplicate keys in the tree, then each subtree contains only things whose keys are less than its right delimiting key. If there are no duplicate keys, then by looking within a node at its pointers to subtrees and their delimiting keys, we know which subtree of that node contains the thing we want.
Duplicate keys are a topic for another time. For now I will only hint that when searching through objects with duplicate keys we find the first of them in the tree. Then we search through all the duplicates, one by one, until we find what we are looking for. Allowing duplicate keys can allow for smaller keys, so there is sometimes a trade-off between key size and the average frequency of such inefficient linear searches.
The contents of each node in the tree are sorted within the node. Therefore, the entire tree is sorted by key, and for a given key we know exactly where to go to find at least one thing with that key.
We choose to make the nodes equal in size, so it is easier to allocate the unused space between nodes, because it will be of a size equal to some multiple of the size of a node. This way, there aren't any problems of space being free but not large enough to store a node. Also, disk drives have an interface that assumes equal size blocks, which they find convenient for their error-correction algorithms.
If having the nodes be equal in size is not very important, perhaps because the tree fits into RAM, then using a class of algorithms called skip lists is worth considering.
Reiser4 nodes are usually equal to the size of a page, which if you use Linux on an Intel CPU is 4,096 (4k) bytes. There is no measured empirical reason to think this size is better than others; it is simply the one that Linux makes easiest and cleanest to program. Quite honestly, we have been too busy to experiment with other sizes.
If nodes are of equal size, how do we store large objects? We chop them into pieces, and we call these pieces items. An item is sized to fit within a single node.
Conventional filesystems store files in whole blocks. Roughly speaking, this means that, on average, half a block of space is wasted per file because not all of the last block of the file is used. If a file is much smaller than a block, the space wasted is a large percentage of the total file size. It is not effective to store such typical database objects as addresses and phone numbers in separately named files in a conventional filesystem because more than 90% of the space in the storage blocks is wasted. By putting multiple items within a single node in Reiser4, we are able to pack multiple small pieces of files into one block. Our space efficiency is roughly 94% for small files. This does not count per-item-formatting overhead, whose percentage of total space consumed depends on average item size and, for that reason, is hard to quantify.
Aligning files to 4k boundaries does have advantages for large files though. When a program wants to operate directly on file data without going through system calls to do it, it can use mmap() to make the file data part of the process' directly accessible address space. Due to some implementation details, mmap() needs file data to be 4k-aligned. If the data is already 4k-aligned, it makes mmap() much more efficient. In Reiser4 the current default is that files larger than 16k are 4k-aligned. We don't yet have enough empirical data and experience to know whether 16k is the optimal default value for this cutoff point.
Continuing with our tree metaphor, leaves are nodes that have no children. Internal nodes are nodes that have children.
A search starts with the root node, traverses two more internal nodes and ends with a leaf node, which is a node that holds the data and has no children.
An item is a data container that is contained entirely within a single node. A node that contains items is called a formatted node. When we store objects in the tree, we put their various parts into items and unformatted leaves. Unformatted leaves (unfleaves) are leaves that contain only data and do not contain any formatting information. Only leaves can contain unformatted data. Pointers are stored in items, and so all internal nodes are necessarily formatted nodes.
Pointers to unfleaves are different in their structure from pointers to formatted nodes. To clarify, extent pointers point to unfleaves. An extent is a sequence of contiguous, in block number order, unfleaves that belong to the same object. An extent pointer contains the starting block number of the extent and a length. Because the extent belongs to only one object, we can store only one key for the extent, and we can calculate the key of any byte within that extent. If the extent is at least two blocks long, extent pointers are more compact than regular node pointers.
Node pointers are pointers to formatted nodes. We do not yet have a compressed version of node pointers, but they should be available soon. Notice that with extent pointers we don't have to store the delimiting key of each node pointed to, while we need to do this when using node pointers. We will probably introduce key compression at the same time we add compressed node pointers. One would expect keys to compress well because they are sorted into ascending order. We expect our node and item plugin infrastructure will make such features easy to add at a later date.
Twigs are parents of leaves, and extent pointers exist only in twigs. (This is a very controversial design decision I will discuss in Part II of this article.) Branches are internal nodes that are not twigs.
You might think we would number the root level 1, but since the tree grows at the top, it turns out to be more useful for number 1 to be the level with the leaves where object data is stored. The height of the tree depends upon how many objects we have to store and what the fanout rate (average number of children) of the internal and twig nodes will be.
Reiser4 includes many different kinds of items designed to hold different types of information:
static_stat_data: holds the owner, permissions, last access time, creation time, last modification time, size and the number of links (names) to the file.
cmpnd_dir_item: holds directory entries and the keys of the files they link to.
extent pointers: explained above.
node pointers: explained above.
bodies: hold parts of files not large enough to be stored in unfleaves.
We call a unit that which we must place as a whole into an item, without splitting it across multiple items. When traversing an item's contents, it is often convenient to do so in units:
For body items the units are bytes.
For directory items the units are directory entries. The directory entries contain a name and a key of the file named (in practice the name and key may be compressed).
For extent items the units are extents. Extent items contain only extents from the same file.
For static_stat_data the whole stat data item is one indivisible unit of fixed size.
I have explained the basic structures of the Reiser4 tree, but the fun stuff is yet to come. I have not yet explained how other researchers structure their trees. Nor did you learn why object contents are stored at the bottom of the tree, why high fanout is important or what are the different kinds of balancing. No hint have I yet given as to why balanced trees are better and dancing trees are best. What I have most especially not done is explain how a subtle and controversial tree structure change, which you can see in the trees depicted in this article, doubled Reiser4 read speed compared to Reiser3. This will (space permitting) be in Part II in next month's issue of Linux Journal.