Learning the iTunesDB File Format

Reverse engineering is one of the skills necessary on many Linux software projects, because many file formats have no open specifications. Even if we have a specification, we will probably have to reverse engineer certain portions to learn all the details. Reverse engineering is a rewarding experience. Not only do we learn something in detail, but it is satisfying to offer Linux users access to previously unsupported devices.

This article discusses the specific example of reverse engineering the iTunesDB file format used by the Apple iPod portable MP3 player. Although this example covers a file format, we can use similar techniques for device drivers and network streams.

The key strategies for reverse engineering are hypothesis, pattern recognition and validation. We use hypotheses to guess what will be in the file. All files contain repeated patterns, and recognizing those patterns is the key to reverse engineering. Validation consists of developing software to check whether a file conforms to a format. If we can tell that a file is valid, we understand the format.

We need a hypothesis for the types of information an unknown file format contains. We know that an iPod plays digital music and the songs can be organized into playlists. Because we can't find any other files on the iPod hard disk for storing this information, we guess that it will be in the iTunesDB file. The goal of trying to find song and playlist information narrows our search when we look for patterns in the file.

Although every file format contains repeated patterns, the trick is recognizing these patterns and learning how to parse them. Opening a file in a hex editor allows us to examine the raw data for patterns. Figure 1 contains the first 256 bytes of an iTunesDB file as shown by Emacs in hexl-mode. The first column is the file position; then there are eight columns, each column containing two bytes. The final column is the ever-helpful ASCII representation of the data.

Figure 1. First 256 Bytes of the iTuneDB File

From only the first 256 bytes, a pattern emerges: three 5-byte sequences start with “mh” (0x6d68). When we scan the rest of the file, we find it littered with 5-byte mh sequences (see Figure 2). Based on the number of mh byte sequences we see in the file, we hypothesize that these sequences are a marker for a data structure. We don't know if the data structure has a fixed or varying size. Perhaps it is only five bytes long and the information between the mh sequences is composed of other data structures. To help us determine this information, we will extract the first 15 mh sequences from the file (Figure 3).

Figure 2. 5-Byte mh Sequences

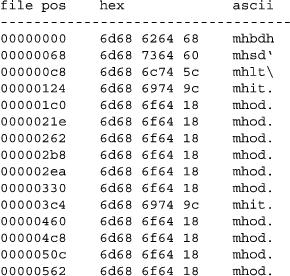
Figure 3. First 15 mh Sequences

The numbers 0x9c and 0x18 do not translate to “.” using ASCII (the ASCII code for . is 0x2e). So, we follow the Emacs example and use . for anything out of the range of standard ASCII characters.

Although we have only a few data points, we find multiple potential patterns. Certain sequences are repeated, such as “mhod.” and “mhit.”. In fact, both of the mhit. sequences are followed by mhod. sequences. Perhaps the patterns exist throughout the file. Before sifting through hundreds of kilobytes in a hex editor, it is a good idea to consider using the third reverse engineering strategy: validation.

A great way to test out hypotheses is to write a validation program, and the sooner the better. The goal of the validation program is to parse the file and determine if it is valid using various tests derived from pattern recognitions and hypotheses. The first iterations of the validation program will have few tests (if any) that are correct, but as we come to understand the format, the program evolves into a compliance tester. It is then useful for checking software that modifies files of this format, because we can use it to ensure that our changes are valid.

Our first validation program will display information (shown in Figure 4) about all the mh chunks in the file to help us find patterns. The first glaring pattern we see pertains to the difference between the file positions of the mh chunks. With the exception of the mhod chunks, the fifth byte contains the number of bytes until the next mh chunk. We can add code to our validation program to check this pattern, and we find that this is almost the case: there are a few chunks besides the mhod chunks that fail our test. It is unlikely that the creators of the iTunesDB file format would limit the size of a data structure to 256 bytes, thus we are probably dealing with a multibyte number.

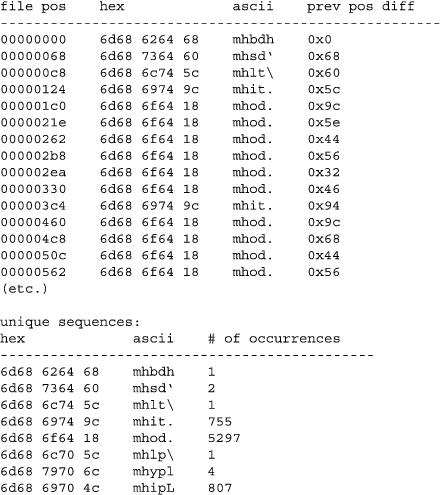
Figure 4. Results of Validation Program

As soon as the word “multibyte” crosses our mind, we must consider the endianness of the file. If this first byte is part of a multibyte number, it is the least significant byte, thus a little endian number. If one number in the file is little-endian, the whole file will be little-endian. Only a sadistic designer would create a mixed-endian file format. Bytes six, seven and eight are almost always zero, so we guess the chunk size is a 4-byte number.

Figure 5 contains a diagram of our theory for the basic building block of the file format. When we change our validation program to use a 4-byte number for the chunk size, the test is successful for all non-mhod chunks.

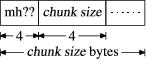
Figure 5. Theory of File Format

Reverse engineering requires us to oscillate between our three strategies in order to decipher the file format. We will continue to employ these strategies to discover more details. We wrote software that can parse the file format into data chunks of variable size and type. We would like to know what every byte in the chunk signifies, and this requires more hypotheses, pattern recognitions and validations.

We start at the top of the file and focus on the mhbd chunk. Given its frequency and its location at the start of the file, it probably contains header information for the whole file. We know it is 0x68 bytes long, and we accounted for only eight of those bytes with our standard tag and chunk length fields. Everything else thus far consists of 4-byte numbers and we have a multiple of four bytes left, so we will break up the remaining 96 bytes into 24 4-byte numbers, as shown in Figure 6.

Figure 6. The Remaining 96 Bytes

The size in bytes of the example iTunesDB file is 571,616. We can add a test to the validation program and verify that n1 is the file size for all iTunesDB files. The n2, n3, n4 trio resembles a version number (1.1.2). Looking at multiple iTunesDB files teaches us that n2 through n4 changes to 1.2.2 for iTunesDB files from newer iPods. n5 to n24 are always zero.

Storing the file size in the header is a curious action. We determined a consistent pattern for the first eight bytes of an mh chunk; perhaps bytes 9-12 are consistent for all mh chunks. We modify our validation program to spit out the value of bytes 9-12 for all mh chunks (see Figure 7 for results).

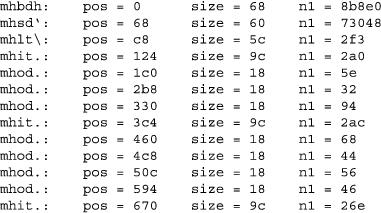
Figure 7. Value of Bytes 9-12

When we add n1 to the file position of the mhbd chunk, we get to the end of the file. Adding n1 to the mhod chunk position is the position of the next mh chunk. For mhsd, adding 0x73048 to 0x68 is 0x730b0. Going to that file position in our hex editor shows us that at 0x730b0 is the start of another mhsd chunk.

The n1 plus file position value for mhit, mhyp and mhip chunks is consistent with the one for mhbd, mhsd and mhod. Figure 8 contains an example of the relationship between these chunks. For mhlt and mhlp, the position at n1 plus the mhlt/mhlp file position is in the middle of a chunk. The n1 value for mhlt in this example is 755, which is the number of mhit chunks in the file. The n1 value for mhlp is 4, which is the number of mhyp chunks. These relationships suggest a nested data structure. If we use the n1 size to determine parent-child relationships between mh chunks, we can create the tree diagram shown in Figure 9. The symmetry looks too good to be wrong, so we'll stick with it as our theory unless we find data later on that convinces us otherwise.

Figure 8. The Relationship between the mhit, mhyp and mhip Chunks and the mhbd, mhsd and mhod Chunks

Figure 9. Parent-Child mh Chunks

Going down the tree one level from mhbd, we have a pair of mhsd nodes, each 104 bytes long. Breaking the data after the initial 12 bytes into 4-byte numbers shows us that only the first 4-byte number contains any non-null data. It equals one when the child node is mhlt and two when the child node is mhlp. Figure 10 contains a description of the mhsd chunk.

Figure 10. The mhsd Chunk

Continuing down to the next level, we find the mhlt and mhlp nodes. We can verify that following the number of children they end with 80 null bytes, as shown in Figure 11.

Figure 11. The mhlt and mhlp Nodes

The children of the mhlt node are mhit nodes. The number of mhit nodes corresponds to the number of songs on the iPod. Dividing the first mhit chunk into 4-byte unsigned integers yields the diagram in Figure 12.

Figure 12. Dividing the First mhit Chunk into 4-byte Unsigned Integers

The only number that looks at all familiar simply by its magnitude is n6. In UNIX, time is usually determined as the number of seconds since the Epoch (00:00:00 UTC, January 1, 1970). In Apple's HFS+ filesystem, however, time is stored as the number of seconds since 00:00:00 UTC, January 1, 1904. Converting 3090924135 to a date yields December 11, 2001, 06:02:15. We can't make much sense of the rest of these numbers yet, but by looking at many mhit chunks we notice that n1 equals the number of mhod children, n3 is always one, and n4 is always zero.

Perhaps by looking at the mhod children of the mhit chunks we can learn what the unknown mhit values signify. Indeed, a cursory look at some mhod chunks (see Figure 13) indicates they contain variable-length text after them.

Figure 13. mhod Children of mhit Chunks

We know that n1 of the mhod chunk (see Figure 14) tells us how long the mhod chunk is including the text data. We need a hypothesis for what the remaining 12 bytes contain.

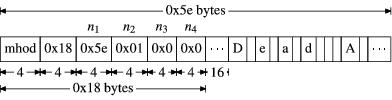
Figure 14. n1 of mhod Chunks

By reading the text, we see the artist, album and title strings are included, among others. The software needs to know what type of string it is for the string to be useful. This information could be provided by always having the strings in the same order: album, title, artist, genre and so on, but what if a song didn't have an album? It is more likely, then, that the type of string is encoded in the chunk somewhere. n2 looks like a good candidate. Looking at the strings and the n2 value, we determine the relationship shown in Table 1.

Table 1. The n2 Value and Description

The text data is not pure ASCII because the letters (in this example) are separated by a null byte. As there are two bytes for every letter, we assume we are dealing with a multibyte representation of text, most likely a Unicode encoding. There are 16 bytes before the text starts, however, that we haven't accounted for them. Figure 15 contains the 16 unknown bytes for the four mhod blocks shown in Figure 13.

Figure 15. The 16 Unknown Bytes for the Four mhod Blocks Shown in Figure 13

We find a 4-byte number that is always one, a varying 4-byte number and 64 bits of zero. On closer inspection, the second number seems to vary with the length of the subsequent string and is, in fact, its length in bytes. We will add a test to our validation program to check if this is true for all mhod strings.

Our validation program finds text data chunks where the first number is zero instead of one. These follow mhod chunks where the type is 100, probably an empty string type. Figure 16 contains a complete description of the mhod chunks.

Figure 16. The Complete mhod Chunk

We can use the mhod children of the mhit chunks to figure out which songs relate to which mhit chunks. This helps us figure out the rest of the mhit chunk: n5 changes based on the file type; n7 is the size of the song's file. n8 is the duration of the song in milliseconds. n9 is the track number. n12 is the bit rate. See Figure 17 for a diagram of the mhit data chunk.

Figure 17. The mhit Data Chunk

Our analysis of the left side of the tree is complete, and using it we can find the information for all the songs on the iPod. Earlier we hypothesized that the other main use of the iTunesDB file is for playlists, so we will look for playlist information in the right side of the tree.

Hoping for symmetry, we want to find one mhyp chunk for each playlist, as there was one mhit chunk for each song. Looking around, we know this iPod has three playlists yet there are four mhyp chunks. When we run our validation program on a variety of iTunesDB files, we learn there is always one more mhyp chunk than the number of playlists.

We will use our validation program to display information about the children of the mhyp chunks. It shows us that every mhyp chunk has a first child that is an empty string mhod chunk (type 100) with a mysterious extra 604 null bytes. Then it has an mhod chunk with a string in it. For the first mhyp chunk, this is the name of the iPod; for every other mhyp chunk it is the name of a playlist.

After the name mhod chunk comes a series of mhip and mhod pairs, until the next mhyp chunk. The mhod portion of the pair is an empty string. The number of these pairs is equal to the number of songs in the playlist. As far as the first playlist is concerned, it has the same number of mhip/mhod pairs as there are songs on the iPod. Thus, we can theorize that this first playlist is a master playlist containing one entry for every song on the iPod.

We know that a playlist is a named list of songs with a title. We found the name already, but we need to figure out how the list of songs is stored. We start by looking at the mhip chunk in Figure 18. n5 is the same order of magnitude as the date we found earlier. We saw n4 (2626) in the mhit data at n2. Thus, we can guess that n4 is a song identification number and that the mhip chunks use song identification numbers to specify which songs are in the playlist. We can add a test to the validation program to match n4 in the mhip chunks, with n2 in the mhit chunks to confirm our theory.

Figure 18. The mhip Chunk

The remaining mhip mystery is that the n3 number is similar in magnitude to the song key, n4. If we change our test program to look for songs whose key is the number following the key we already found, we won't find any songs with these identification numbers in any iTunesDB file. We can deduce, then, that it is a unique identification number for these chunks. Adding a test to our validation program confirms they are indeed unique. Figure 19 contains a diagram of the mhip data chunk.

Figure 19. The mhip Data Chunk

The mhyp chunk (see Figure 20) is the final chunk we need to evaluate. n1 is always 2. n2 is the number of songs in the playlist. The master playlist has n3 set to 1; all other playlists have it set to 0. n4 is a date, probably the date the playlist was created. n5 and n6 are the same for every mhyp chunk, and 72 null bytes always follow them.

Figure 20. The mhyp Chunk

Using the three reverse engineering strategies of hypothesis, pattern recognition and validation, we deciphered the iTunesDB file format. Hopefully the ideas presented here will help Linux users reverse engineer more devices and file formats to make them compatible with Linux.