
Version 4 of the Reiser filesystem flattens the tree data structure fo rbetter performance than version 3. Here's how it's structured.
This article is the second in a series on the design of the Reiser4 filesystem. The first article [LJ, December 2002] defined basic concepts: trees, nodes and items. This article explains why balanced trees are better than unbalanced trees and why B+trees are better than B-trees by explaining and applying the principles of caching. The article then applies these same principles to a classic database technique used in ReiserFS v3 called binary large objects (BLOBs). It suggests that BLOBs reduce the effectiveness of caching internal nodes by making the tree no longer truly balanced. It also shows how Reiser4 stores objects larger than a node without unbalancing the tree.
I apologize to readers for the delay of this article, which is due to the Halloween feature-freeze for 2.6 and the need to stabilize Reiser4 quickly at that time.
The fanout rate (n) refers to the number of nodes pointed to by each level's nodes (Figure 1). If each node can point to n nodes of the level below it, then starting from the top, the root node points to n internal nodes at the next level, each of which points to n more internal nodes at its next level and so on. m levels of internal nodes can point to nm leaf nodes containing items in the last level. The more you want to store in the tree, the larger you have to make the fields in the key that first distinguish the objects, then select parts of the object (the offsets). This means your keys must be larger, which decreases fanout (unless you compress your keys, but that will wait for our next version).
In Figure 1, the first graph is a four-level tree with a fanout of n = 1. It has only four nodes, starting with the (red) root node, traversing the (burgundy) internal and (blue) twig nodes and ending with the (green) leaf node, which contains the data. The second tree, with four levels and a fanout of n = 2, starts with a root node, traverses two internal nodes, each of which points to two twig nodes (for a total of four twig nodes) and each of these points to two leaf nodes for a total of eight leaf nodes. Lastly, a four-level, fanout of n = 3 tree is shown, which has one root node, three internal nodes, nine twig nodes and 27 leaf nodes.
You can store not only pointers and keys in internal nodes but also the objects to which those keys correspond. This is what the original B-tree algorithms did (Figure 2).
Then, B+trees were invented that have only pointers and keys stored in internal nodes with all of the objects stored at the leaf level (Figure 3).
Fanout is increased when we put only pointers and keys in internal nodes and don't dilute them with object data. Increased fanout raises our ability to cache all of the internal nodes, because there are fewer internal nodes. People often respond to this by saying, “but B-trees cache objects, and caching objects is just as valuable.” This is not, on average, the answer. Of course, discussing averages makes the discussion much more difficult.
However, we need to cover some cache design principles before getting to this. Let's suppose the following:
You have two sets of things, A and B.
You need things from those two sets semi-randomly, with a tendency for some things to be needed much more frequently than others, but which things those are can shift over time.
You can keep things around after you use them in a cache of limited size.
You tie the caching of each thing from A to the caching of some particular thing from B. This means that whenever you fetch something from A into the cache, you fetch its partner from B into the cache.
This increases the amount of cache required to store everything recently accessed from A. If there is a strong correlation between the need for the two particular objects that are tied in each of the pairings, stronger than the gain from spending those cache resources on caching more members of A and B according to the LRU (least recently used) algorithm, then this might be worthwhile. If no such strong correlation exists, it is bad. LRU means that we choose the least recently used thing to discard from the cache when we need to make more room. Various approximations of LRU are the most commonly used caching algorithms in OS design.
But wait, you might say, you need things from B also, so it is good that some of them were cached. Yes, you need some random subset of B. The problem is that without a correlation, the things from B that you need are not especially likely to be those same things from B that were tied to the things from A that were needed. Choosing what from B you bring into the cache and keep in the cache on the basis of something other than LRU may reduce the effectiveness of caching, unless it is done according to an algorithm at least as good as LRU. Often choosing which members of B to cache based on which members of A have been cached is not as good as LRU, and so we have a problem.
This tendency to inefficiently tie things that are randomly needed exists outside the computer industry. For instance, suppose you like both popcorn and sushi, with your need for them on a particular day being random. Suppose that you like movies randomly. Suppose a theater requires you to eat only popcorn while watching the movie you randomly found optimal to watch, and not eat sushi from the restaurant on the corner while watching that movie. Is this a socially optimum system? Suppose quality is randomly distributed across all hot dog vendors. If you can only eat the hot dog produced by the best movie displayer on a particular night that you want to watch a movie, and you aren't allowed to bring in hot dogs from outside the movie theater, is this a socially optimum system? Optimal for you?
Tying strongly correlated things together can sometimes be good for performance, however. Many filesystems tie access to information about the file's size to information about the file's name. This seems to work well, better than LRU would.
Tying uncorrelated things together is a common error in designing caches but is still not enough to describe why B+trees are better. With internal nodes, we store more than one pointer per node, meaning pointers are not cached separately. You could argue that pointers and the objects to which they point are more strongly correlated than the different pointers. I hope what we have discussed here is instructive, but we still need another cache design principle.
Let the cache temperature of something be equal to how often you access it, times the average cost to fetch it from disk, divided by the number of bytes of cache it consumes. You may notice a certain careful lack of precise detail in this definition—particularly, how small objects read individually tend to be hotter because of the cost of performing seeks. Other definitions of cache temperature are possible, but this one is most convenient for this article.
If two types of things cached in nodes have different average temperatures, segregating them into separate nodes helps caching. Suppose you have R bytes of RAM for cache and D bytes of disk. Suppose that 80% of accesses are to the most recently used things that are stored in H (hotset) bytes of nodes. Reducing the size of H so it is smaller than R is important for performance. If you disperse your frequently accessed data evenly, a larger cache is required, and caching is less effective.
If, all else being equal, we increase the variation in temperature among all nodes, we increase the effectiveness of using a fast small cache.
If two types of things have different average temperatures, separating them into separate nodes increases the variation in temperature in the system as a whole.
If all else is equal, and if two types of things cached several to a node have different average temperatures, segregating them into separate nodes instead helps caching.
Pointers to nodes frequently tend to be accessed relative to the number of bytes required to cache them. Consider that you have to use the pointers for all tree traversals that reach the nodes beneath them, and that they are smaller than the nodes to which they point.
Putting only node pointers and delimiting keys into internal nodes concentrates the pointers. Because pointers tend to be two orders of magnitude more frequently accessed per byte of their size than items storing file bodies, a high average temperature difference exists between pointers and object data.
According to the caching principles described previously, segregating these two types of things with different average temperatures (pointers and object data) increases the efficiency of caching.
Now you might say, why not segregate by actual temperature instead of by type, because type correlates only with temperature? We do what we can easily and effectively code, with not only temperature segregation in consideration. Some tree designs rearrange the tree so that objects with a higher temperature are higher in the tree than pointers with a lower temperature. The difference in average temperature between object data and pointers to nodes is so high that I don't find such designs a compelling optimization, plus they add complexity. Given the two order of magnitude average temperature difference, I suspect that if I am wrong it is not by enough to care about.
On a side note, although these other tree designs just mentioned migrate objects higher in the tree according to temperature, if one was merely to segregate by temperature without changing levels, it might be more effective. If one had no compelling semantic basis for aggregating objects near each other (this is true for some applications), and if one wanted to access objects by nodes rather than individually, it would be interesting to have a node repacker sort object data into nodes by temperature.
B+trees separate the pointers and the data into different nodes. On average, the pointers to the nodes of the tree are hotter than the data of the things stored in the tree (by about two orders of magnitude). Therefore, according to the principles of caching explained previously, caching is improved by separating the pointers to nodes from the data of things stored in the tree.
In the industry, B+trees are known in practice to be better than B-trees, exactly as this theory predicts. It is also accepted wisdom that balanced trees perform better than unbalanced trees.
What is not currently accepted wisdom, but is predicted by the application of these principles, is that the use of, what are called by the database industry, BLOBs hurts performance. More on that (and what BLOBs are) in a bit.
The term balanced is used for several distinct purposes in balanced tree literature. Two of the most common are balanced height and balanced space usage within the nodes of the tree. Unfortunately, these different definitions are a classic source of confusion for readers of the literature, and I'll try to avoid that in this article.
Height-balanced trees are those for which each possible search path from root node to leaf node has exactly the same length; length equals the number of nodes traversed from root node to leaf node. For instance, the height of the tree in Figure 1 is four, the height of the tree in Figure 4 is three and the height of the single-node tree is one.
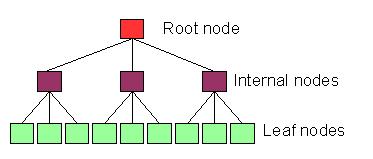
Figure 4. A Three-Level Tree
Most algorithms for accomplishing height balancing do so by growing the tree only at the top. Thus, the tree never gets out of height balance.
Figure 5 shows an unbalanced tree. It originally could have been balanced and then lost some of its internal nodes due to deletion, or it could have been balanced once but now be growing by insertion, without yet undergoing rebalancing.
Traditional database methods for storing objects larger than nodes (BLOBs) make trees unbalanced. BLOBs are a method of storing objects larger than a node by storing pointers to nodes containing the object. These pointers commonly are stored in what are called the leaf nodes (level 1, except that the BLOBs are then sort of a basement “level B”) of a “B*” tree.
In Figure 6, a BLOB has been inserted into a leaf node of a four-level tree, meaning pointers to blocks containing the file data have been inserted into the leaf node. This is what a ReiserFS v3 tree looks like.
This is a significant definitional drift, albeit one accepted by the entire database community. By the principles of caching described here, this reduces the separation of pointers and object data, which in turn reduces the effectiveness of caching. I suggest that those principles of caching indicate it is a bad design. For all of the reasons that B+trees are better than B-trees, Reiser4 trees are better than ReiserFS v3 trees, though to a less extreme amount.
By contrast, Figure 7 is a Reiser4 tree with a fanout of three, a BLOB in the level-one leaf nodes and the pointer to it in the level-three twig nodes. In this case, the BLOB's blocks are all contiguous. For reasons of space, it is set below the other leaf nodes, but its extent pointer is in a level-two twig node, like every other item's pointer.
Although it is accepted that B+trees are better than B-trees, it is not well accepted that BLOBs are a bad design, and indeed, it is the dominant paradigm within the database industry.
Gray and Reuter say the criterion for searching external memory is to “minimize the number of different pages along the average (or longest) search path....by reducing the number of different pages for an arbitrary search path, the probability of having to read a block from disk is reduced” (see Resources).
My problem with this explanation of the effectiveness of the height-balanced approach is it does not convey that you can get away with having a moderately unbalanced tree, provided you do not significantly increase the total number of internal nodes. In practice, most unbalanced trees do have significantly more internal nodes. In practice, most moderately unbalanced trees have a moderate increase in the cost of in-memory tree-traversals and an immoderate increase in the amount of I/O due to the increased number of internal nodes not remaining in cache because there are now too many of them.
But, if one were to put all the BLOBs together in the same location in the tree, because the amount of internal nodes would not significantly increase, the performance penalty for having them on a lower level of the tree than all other leaf nodes would not be a significant additional I/O cost. There would be a moderate increase in that part of the tree traversal time cost, which is dependent on RAM speed, but this would not be so critical. Segregating BLOBs could perhaps substantially recover the performance lost by architects not noticing the drift in the definition of height balancing for trees. There might also be a substantial I/O-related performance effect for segregating BLOBs that is unrelated to tree considerations. Perhaps someday someone will try it and tell us what happens.
Reiser4 returns to the classical definition of a height-balanced tree in which the lengths of the paths to all leaf nodes are equal. It does not pretend that all of the nodes storing objects larger than a node are somehow not part of the tree, even though the tree stores pointers to them.
Reiser4 reduces the number of internal nodes, nodes containing pointers, from the number required for ReiserFS v3. The number of internal nodes required for ReiserFS v3 to store the 188MB Linux kernel 2.4.1 source code tree is 1,629. Reiser4 requires only 164. As a result, the amount of RAM required to store pointers to nodes is reduced dramatically in Reiser4.
In upcoming articles we will discuss why, even when nothing is cached in memory, Reiser4's performance is much higher than that of ReiserFS v3, why dancing trees are better than space-usage balanced trees and how we added support for transactions while at the same time greatly reducing the amount of data that is written twice.