 | Chapter 4: Graphics with AWT and Java 2D |  |

As we discussed earlier when we considered the Java 2D coordinate system, the java.awt.geom.AffineTransform class represents a general mapping from one coordinate system to another. AffineTransform defines a general coordinate-system transformation that can include translation, scaling, rotation, and shearing.
One of the easiest ways to obtain an AffineTransform object is to use one of the static methods defined by AffineTransform. For example, getScaleInstance() returns an instance of AffineTransform that represents a simple scaling transformation.
Another way to get an AffineTransform is with the AffineTransform() constructor, of course. The no-argument version of the constructor returns an AffineTransform that represents the identity transform--that is, no transform at all. You can modify this empty transform with a number of methods. Note that AffineTransform defines several other constructors, but we have to wait to discuss them until after we've discussed the mathematics that underlie AffineTransform.
Once you have obtained an AffineTransform object, you can modify it with methods just like the methods defined by Graphics2D. Each of the translate(), scale(), rotate(), and shear() methods modifies an AffineTransform by adding the specified transformation to it. Note that there are two versions of rotate(). One rotates around the origin and the other rotates around a specified point; both use angles specified in radians. Remember that calls to these four methods are cumulative: you can build up a complex transformation as a combination of translation, scaling, rotation, and shearing.
AffineTransform also defines noncumulative methods. setToTranslation(), setToScale(), setToRotation(), and setToShear() set an AffineTransform to a single transform, replacing whatever transform was previously contained by the AffineTransform.
Once you have created and initialized an AffineTransform object, you can use it to transform points and shapes. AffineTransform defines a number of transform() methods that transform points represented by either java.awt. geom.Point2D objects or arrays of numbers. deltaTransform() is a variant of transform() that performs a transformation disregarding any translation component. It is designed for transforming distances or position-independent vectors, instead of actual points. inverseTransform() is the inverse of transform()--it converts points expressed in the new coordinate system back to the corresponding points in the original coordinate system.
The transform(), deltaTransform(), and inverseTransform() methods are fairly low-level and typically are not used directly by Java 2D programs. Instead, a program typically uses the createTransformedShape() method, which provides a powerful, high-level transformation capability. Given an arbitrary Shape object, this method returns a new Shape that has been transformed as specified by the AffineTransform object.
The coordinate system transformations described by AffineTransform have two very important properties:
Straight lines remain straight
Parallel lines remain parallel
An AffineTransform is a linear transform, so
the transformation can be expressed in the matrix notation of
linear algebra. An arbitrary AffineTransform
can be mathematically expressed by six numbers arranged in a
matrix like this:
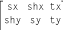 In this matrix, tx and ty
are the translation amounts,
sx and sy are the scaling
factors, and shx
and shy are the shearing factors, all in the
X and Y dimensions, respectively.
As we'll see in a moment, rotation is a combination of
scaling and
shearing, so there are not separate
rx and ry numbers.
In this matrix, tx and ty
are the translation amounts,
sx and sy are the scaling
factors, and shx
and shy are the shearing factors, all in the
X and Y dimensions, respectively.
As we'll see in a moment, rotation is a combination of
scaling and
shearing, so there are not separate
rx and ry numbers.
To transform a point from one coordinate system to another using
an AffineTransform, we multiply the point by
this matrix. Using matrix notation (and adding a few dummy
matrix elements), the equation looks like this:
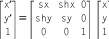 This matrix equation is simply shorthand for the following
system of equations:
This matrix equation is simply shorthand for the following
system of equations:
x' = sx*x + shx*y + tx y' = shy*x + sy*y + ty
The identity transform does not perform any
transformation at all. It looks like this:
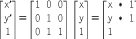
Mathematically, rotation is a
combination of scaling and shearing. The rotation of an angle
theta around the origin is expressed with a
matrix like this:
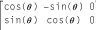 You don't need to understand how this rotation matrix works. If
you remember basic trigonometry, however, you can use it
and the preceding equations to verify that this matrix works for the
base cases of 90-degree and 180-degree rotations.
You don't need to understand how this rotation matrix works. If
you remember basic trigonometry, however, you can use it
and the preceding equations to verify that this matrix works for the
base cases of 90-degree and 180-degree rotations.
As we've seen, it is possible to make cumulative changes to an
AffineTransform. This is done by multiplying
the current transformation matrix by the new transformation
matrix. For example, suppose we perform a translation by
100 units in both the X and Y dimensions and follow this by
scaling both the X and Y dimensions by a factor of 2. The
resulting AffineTransform matrix is the
product of the two individual matrices:
 Note that matrix multiplication is not commutative. If we
perform the scaling operation first and then do the
translation, we obtain a different result:
Note that matrix multiplication is not commutative. If we
perform the scaling operation first and then do the
translation, we obtain a different result:
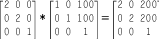
Most applications do not have to work with matrices explicitly in order to perform coordinate-system transformations. As we've seen, it typically is easier to use the translate(), scale(), rotate(), and shear() methods of either AffineTransform or Graphics2D. It is useful to understand the mathematics underlying AffineTransform, however.
You may, on occasion, have the need to create a
custom AffineTransform object from a set of
six numbers. A number of AffineTransform
constructors and methods take matrix elements as arguments.
These matrix elements are either passed in explicitly or
specified in an array. Note that the matrix-element naming
system used by the AffineTransform class is
different than the system I've used here. The parameter names
for AffineTransform methods are based on the
following matrix:
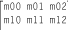 This is nothing more that a different naming scheme for the
elements we are already familiar with:
This is nothing more that a different naming scheme for the
elements we are already familiar with:
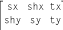 When matrix elements are passed to or returned by an
AffineTransform in an array of
float or double values,
they are stored in this order:
When matrix elements are passed to or returned by an
AffineTransform in an array of
float or double values,
they are stored in this order:
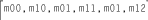 This corresponds to the following order using our mnemonic names:
This corresponds to the following order using our mnemonic names:
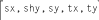

Copyright © 2001 O'Reilly & Associates. All rights reserved.