
An essay on the aesthetics of polygons and algorithms that one might see in a web image map.
Several algorithms exist in the public domain for web servers to determine whether a point is inside a polygon. They are used in the implementation of “image maps”, both of the traditional server-side variety as well as those of the more modern client-side. So who needs one more? Well, the bone this author wishes to respectfully pick is that most of the point-in-polygon code he could find is woefully over-complicated. Being a lover of simplicity and simplification, he just could not leave well enough alone.
The resulting C-language routine has just three if statements and no divides. Contrast that with three divides and ten if statements in the corresponding routine that's part of the popular Apache web server. Get the Apache distribution and search for pointinpoly to see the whole works. The routine from CERN/W3C's httpd is even worse, weighing in at 19 if statements! Search for inside_poly in their HTImage.c. (The URLs are shown in Table 2.)
Table 1 contrasts five different routines in the public domain for finding out if a point is in a polygon. In all cases, the polygon is specified as an array of X,Y coordinates of the corner points.
Table 1. Comparison of Point-in-Polygon Algorithms
This is a pretty casual analysis of the algorithms. I certainly didn't shy away from showing my inpoly() in a good light. For example, && and || operators in C are often statements in disguise. I used one of these operators (as did most of the other folks), but that doesn't show up in the table at all. Also, some line counts are inflated slightly by comments and blank lines. But you get a rough idea.
Table 2. Sources of Public Domain Point-in-Polygon Algorithms
All judgments have a context, and I should explain mine. The primary prerogative in this article is algorithmic simplicity. This, I confess, has very little to do with the practical needs of the Web. In case I've gotten ahead of myself, a web image map is a way of carving up an image so that clicking in one particular region does one thing, and clicking somewhere else does something else. Web image maps are such a tiny fraction of the work of web servers and browsers that all of the above routines are just fine as they are. Changing from one to another is not going to make any noticeable difference in web performance. And once we're sure it works, who's going to look at the code again for 100 years? Thus I don't have any practical considerations of performance or readability to justify my cause. I'm simply championing the aesthetics of simplicity.
The point I wish to make is that problems are not always what they seem. Sometimes a simple solution exists, but you've got to take a hard look to find it. My buddy Craig had started out by porting inside_poly() from W3C, I think it was, for use on our web server. When I saw all the floating point math and if statement special cases, I thought there had to be a better way. So Craig and I started from scratch, wrestled the problem to the ground, and came up with a solution containing no floating point math, which is silly for screen pixels, and no math more tedious than multiplication. We also got rid of all the pesky special cases, except for one: polygons with fewer than three sides are excluded. What could be inside a two-sided polygon? Apache's pointinpoly() doesn't even check, and probably makes a big mess with a one-point polygon.
Now, the stated goal is simplicity, not performance, but I did stray from that course on one issue: avoiding divides. Again, performance hardly matters for image map applications, but one day someone might use this algorithm for some kind of 3D hidden surface algorithm or something. Getting rid of the divide may have, in effect, required me to use an additional if statement. Anyhow, what all this is leading up to is that Kevin Kenny's algorithm (see Table 1) at 29 lines and two if statements is by far the shortest and simplest. But mine is still better in some sense, because mine doesn't need a divide and his does.
Now let's discuss the more popular algorithm for determining whether a point is inside a polygon.
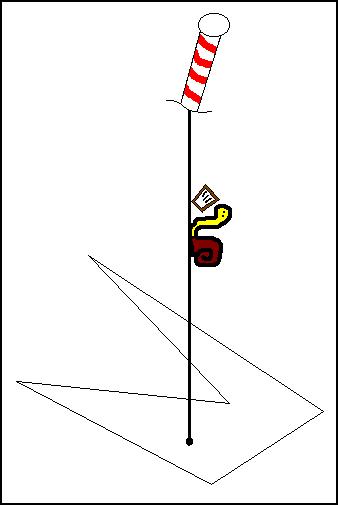
Figure 1. An Odd Number of Polygon Crossings
Imagine you could detect whether a point was in a polygon or not by placing a friendly trained snail at the point and telling him to head for the North Pole. (We're only concerned with image maps, so we exclude polygons that extend to the North Pole, and we ignore Coriolis forces.) You'd equip our intrepid friend in Figure 1 with a snail-sized clipboard and instruct him to tick off each time he crossed an edge of the polygon. He'd call you from the North Pole and report the number of crossings. An even number (including zero) means he started outside the polygon, odd means inside.
This reduces the problem to detecting whether or not line segments intersect. It's even a little better than that, because one of the line segments is simply the positive Y axis. To make that leap, just declare the snail's starting point to be the origin, (0,0), and translate all of the polygon corners so they're relative to that point.
We'll go into the algorithm a little later, but take a look at the finished code in Listing 1. The very picture of simplicity, right? If you haven't checked out the other versions, you really ought to.
The test program (Listing 2) draws a random 40-sided polygon and then picks random points to throw at the inpoly() routine. Points the routine says are inside the polygon it draws red, points outside are blue.
Our first rendition of inpoly() had a subtle flaw which the test program made evident. The full story contains an embarrassing lesson. “It'll work,” we sneered, “We don't need to waste time on a full graphical test. Besides, it'd be too much fun.” After we found out our image maps had leaks, we wrote the test program. Figure 3 shows a close-up of the flaw.
Along a vertical line, all the colors are wrong. The flaw turned out to be that when our mindless mollusk crosses the bottom corner, the little hummer was counting the crossing of both edges! After that, he was always exactly wrong—he thought he was in when he was out, and he thought he was out when he was in. The solution must ensure that when our esteemed escargot crosses into the polygon corner, he counts exactly one crossing. Two is no good, and in fact, zero is just as bad—one is what we need. The reason the flaw in the close-up extends up from the corner is that the positive Y axis extends downward in screen coordinates.
I suspect this is a problem unique to the fixed-point world. I'm sure my fellow point-in-polygon smiths have either lucked out or dealt with it somehow. At least, I'd like to think so. (A lie-detector would peg me on that one. This article would be insufferably smug if I had found leaky corners in any of the other algorithms.) In my case, I realized I could not blindly count all crossings of the end point of each of the edges as a crossing. My first thought was to associate each end point with one—and only one—edge. This sounds fair and equitable, but like many things fitting that description, it just plain won't work. A problem turns up when Agent Snail just lightly nicks the corner of a polygon he's not inside at all. That's counted as one crossing, hence the snail report is bunk.
Since I abhor special cases, I sought something that would work in all cases.
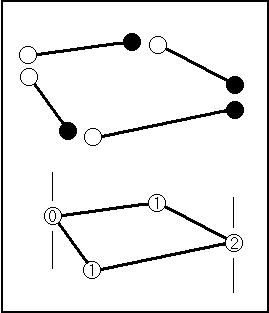
Figure 4. Counting Only the Right End of Each Edge
The scheme for getting our faithful friend to count corner crossings correctly is to always count a crossing of the right end of each edge, but never the left end (right meaning positive X). In the figure, the black circles represent points our snail will count if he crosses; the white circles he won't count. When you put the polygon together, everything ends up the way we want. Nicking the corner means he counts either 0 crossings or two crossings. We don't care which; both are even and our snail knows he's outside. The circles with ones in them represent points counted once if the snail crosses them. This is fine, just like crossing the nearby sides.
It's time to analyze the guts of the inpoly() routine in Listing 3. This represents a slight modification of the snail's instructions. He plays a bit of a “she loves me, she loves me not” kind of game rather than counting up the crossings and then reporting whether the total is even or odd. He starts out assuming he's outside, and complements that assumption with each crossing. So much for the inside=!inside statement.
Listing 3. The “Guts” of the inpoly() Routine
This if test happens inside a for loop that considers all of the edges of the polygon, one at a time. Each edge is a line segment that stretches between the corners (xold,yold) and (xnew,ynew). We've arranged it so (x1,y1) and (x2,y2) also represent the same edge, but the points are swapped, if necessary, to make it so x1 <= x2.
Now two things must be true for our ever-meticulous snail to count the crossing of this edge. First, the segment must straddle the Y axis (where the right end is counted but the left one is not). Second, straddling has to happen to the north of the snail's starting point. These are exactly the questions determined by the if statement's two pieces, on either side of the &&.
Now that first expression is a sneaky one, and I confess I might have preferred the less opaque code (x1 < xt && xt <= x2). You can see it does the same thing if you look carefully (very carefully—I was fooled for a while there). But I hate to fix something unless I've already broken it, if you know what I mean.
That north computation is the one I'm proud of because none of my esteemed fellow polygon smiths made one that doesn't need a divide. It does depend on the knowledge that (x2-x1) is positive. Other than that, it's just a transmogrification of that famous y=mx+b equation from high school algebra.
By the way, I've left out the case where an edge line segment stands straight up and down above the snail touchdown point. Such an edge would never be counted by Mr. Snail at all! That's because the == test would always be false, since xnew, xt and xold are all the same value. What's really wild is that's just what we want. In a sense, he's crossing three edges when we only want to count one. It turns out the adjacent line segment crossings are all we're interested in, and the rules already discussed work perfectly for them.
By the way, who cares whether the points in an image map along the edge of a polygon are technically inside or outside? As you can see in the close-up, some of the originally white pixels (representing the polygon edge) turned to red, others to blue. If a browsing user clicks on the edge of a region, he may get in, he may not. But being one pixel off is usually not an issue if your screen resolution is greater than 100 x 100. In the inpoly() routine, some edges are in, some are out. (I don't mind admitting to a crime after convincing everyone it deserves no punishment.)
I haven't discussed the angle-sum method used by Woods Hole Oceanographic Institution for their algorithm written in Matlab. The algorithm needs to compute arc-tangents, so it's mostly just a laboratory curiosity. The idea is that you add up the angles subtended by lines drawn from the target point to each of the corners of the polygon. If the sum is an even multiple of 360 degrees, you're out; odd, you're in. Vaguely familiar? Here's the analogy: You're in a pitch-black room with a very, very long snake all over the floor. This is a particularly rare variety of deep sea snake (Woods Hole knows all about them) with glow-in-the-dark dots every foot or so. Oh, and he reacts to light by instantly constricting in an iron grip of death. Your question is whether you're standing inside the maze of coils at your feet or outside. You'd like to know before you turn on the light because he gets very annoyed if you step on him.
Face the head of the snake and visually trace his entire body, somehow noting as you do how your feet turn (it's a stretch I know). When you're done, face the head again. Now, if you didn't have to turn around at all, you're safely outside the snake. If you turned around twice in either direction things are fine too. Four times, and you're still OK. If you turned around an odd number of times in either direction, you're meat—no wonder folks tend to use the crossing-count algorithm.