
Classical cryptography provides security based on unproven mathematical assumptions and depends on the technology available to an eavesdropper. But, these things might not be enough in the near future to guarantee cyber security. We need something that provides unconditional security. We need quantum cryptography.
Imagine you want to send a message to your friend, and you don't want others to be able to read the message. You lock your message in a box using a key and send the box to your friend. Your friend also has a key to unlock that box, so he easily can open the box and read the message. In general, this is the technique used by cryptographic algorithms. Locking the message in the box is like encryption, and unlocking the box is like decryption. Before sending the message to the receiver, the data is encrypted using an encryption algorithm and a secret key. On the receiver side, the encrypted data is decrypted using the reverse encryption algorithm.
Classical cryptographic algorithms mostly rely on mathematical approaches to secure key transmission. The security they offer is based on unproven assumptions and depends on the technology available to an eavesdropper. But, rapidly growing parallel and quantum technologies may be a threat to these classical cryptography techniques in the near future. One of the solutions to these threats is quantum cryptography.
What is quantum cryptography? Quantum cryptography is a complex topic, because it brings into play something most people find hard to understand—quantum mechanics. So first, let's focus on some basic quantum physics that you'll need to know to understand this article.
Quantum, in physics, is a discrete natural unit, or packet of energy, charge, angular momentum or other physical property. Light, for example, appears in some respects as a continuous electromagnetic wave, but on the submicroscopic level, it is emitted and absorbed in discrete amounts or quanta. These particle-like packets (quanta) of light are called photons, a term also applicable to quanta of other forms of electromagnetic energy, such as X rays and gamma rays.
One unique thing about quanta is that they can exist in all of their possible states at once. This also applies to photons. This means that in whatever direction a photon can spin—say, diagonally, vertically and horizontally—it does so all at once. Quantum of light in this state is called unpolarized photons. This is like someone moving north, south, east, west, up and down all at the same time. This property is called superposition. One thing you should keep in mind is that measuring something that is in its superposition causes it to collapse into a definite state (one of all the possible states). Figure 1 should help describe superposition.
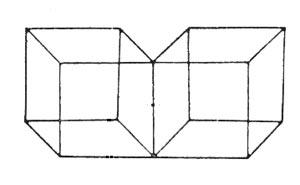
Figure 1. Necker Cubes
Looking at Figure 1, you can identify one of four possibilities: either both squares are protruding forward or both are backward, or one is forward and the other is backward. Each time you look at the diagram, only one possibility is true. In a sense, all four options exist together, but when you look at the diagram, it collapses into just one. This is the essence of quantum superposition.
Through the use of polarization filters, you can force the photon to take one of its states, or technically, polarize it. If you use a vertical polarizing filter, some photons will be absorbed, and some will emerge on the other side of the filter. Those photons that aren't absorbed will emerge on the other side with a vertical spin. Thus, you can polarize the photons to your required orientation using suitable filters.
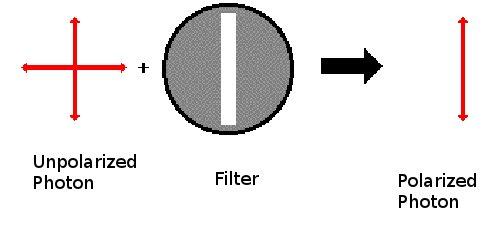
Figure 2. Polarizing Photons
The foundation of quantum physics is the unpredictability factor. This unpredictability is pretty much defined by Heisenberg's Uncertainty Principle. This principle says that certain pairs of physical properties are related in such a way that measuring one property prevents the observer from knowing the value of the other. But, when dealing with photons for encryption, Heisenberg's Principle can be used to your advantage. When measuring the polarization of a photon, the choice of what direction to measure affects all subsequent measurements. The thing about photons is that once they are polarized, they can't be measured accurately again, except by a filter like the one that initially produced their current spin. So if a photon with a vertical spin is measured through a diagonal filter, either the photon won't pass through the filter or the filter will affect the photon's behavior, causing it to take a diagonal spin. In this sense, the information on the photon's original polarization is lost.
In the diagram in Figure 3, I have used the wrong basis for the last two cases, and you can see that I have changed the polarization of two photons.
The bit is the fundamental concept of classical computation and classical information. Quantum computation and quantum information are built upon an analogous concept: the quantum bit, or qbit for short. Just as a classical bit has a state of either 0 or 1, a qbit is like a bit, but it is in superposition between 0 and 1. Two possible states for a qbit are the states “|0 >” and “|1 >” . This notation is called Dirac notation. A qbit can be fully expressed as: a|0 > +b|1 > with a2 + b2 = 1. When we measure a qbit, we get a 0 with probability a2 and 1 with b2.
Now consider a quantum computer with two qbits. There are four possible states: |00 >, |01 >, |10 > and |11 >, and its superposition is a|00>+b|01>+c|10>+d|11>, where a2, b2, c2 and d2 are the probabilities of finding two qbits in any of the four states. In a quantum computer, the two bits are in all possible states at one time. So it is possible to add a number to the two bits, which means we can add the number to 00,01,10,11 and compute the result at the same time. This ability to operate on all states at one time makes it so powerful.
Here the number of parallel operations depends on the number of qbits used. If N number of qbits are used, then 2N operations can be done in parallel, and this inherent parallelism makes quantum computers so fast. But the question is, how do you encode a photon as a qbit? We know a photon has its own spin in all possible directions. As in certain digital systems, we consider +5 volts as 1 and 0 volts as 0, and we can use the spin property of a photon to encode a photon as a qbit. We can use the photon's spin in a particular direction as 1 and the spin in the other direction as 0—say, a photon with vertical spin will be considered as 1 and a photon with an angular spin as 0.
Before starting to describe what quantum cryptography is, let me introduce three names I use throughout this article: Alice, Bob and Eve. Alice is sending the message, and Bob is receiving the message. Eve is in between them, trying to intercept the message. What Eve does is somehow collect the secret key to the message and decrypts it. Now, if Alice somehow can send the key of the message to Bob without any interception, she can send the message without problems.
Now, let me discuss the BB84 protocol. It is based on the name of the inventors Charles Bennet and Gilles Brassard, and it was invented in 1984. Quantum cryptography follows two steps. The first one is sending the secret key, and the second step is sending the message. Here, Alice and Bob make use of two fundamentally different communication channels: a classical channel and a quantum channel. A classical channel is something that you use on the Internet to transfer data. In a classical channel, Eve can observe the bit-stream without affecting the data. But, a quantum channel is something different. It is capable of sending information in terms of quantum, and Eve can't observe the data without affecting the data. In the BB84 protocol, the secret key is sent through the quantum channel, but the message is sent through the ordinary channel but encrypted by the secret key. The first step is called Quantum Key Distribution (QKD). In this step, Alice and Bob use the quantum channel for communication.
First, let's imagine there is no Eve between Alice and Bob. Let's assume that Alice is using two types of polarizer: one is a diagonal polarizer (X) and one a rectilinear polarizer (+). In a rectilinear basis, a photon with a spin “|” (that is, up to down ) is considered as 1, and a “-” (that is, left to right) is 0. In a diagonal basis, a photon with a spin “/” is considered as 1, and “\” is 0. The diagram shown in Figure 5 should help you understand how I'm representing photons as binary values.
Now Alice has a key, and for each bit, she will select a random basis (either diagonal or rectilinear) to encode the bit to send. Nobody, not even Bob, knows what basis Alice is using. Bob will receive the encoded qbits, and Bob will use random basis to decode the qbits. If he uses the same basis, he will get the exact bit that Alice sent; otherwise, there is a 50% chance that he will get a wrong bit. For example, if Alice uses a diagonal basis to encode 1, and Bob also uses diagonal basis to decode that, then he will get a 1. If he uses a rectilinear basis, then there is a 50% chance that he will get a 1 and a 50% chance of getting 0. As Bob is also using random basis, there's a 50% chance that he will use the right basis (that is, he will use the basis that Alice used) and will decode 50% of qbits exactly, and for the 50% wrong basis, he will decode 25% of qbits exactly, and that means Bob will decode 75% of qbits exactly.
Alice and Bob will exchange the basis they used for each bit using the normal channel without revealing their bits. They can check for which bits they both used the same basis, and those bits will be used as the secret key. Consider the example shown in Table 1 where Alice is sending the secret key 100101.
In this case, Bob will decode the key as 1,0/1,0,0/1,0/1,1. Because Bob has used some wrong basis to measure the qbits, he may get a 0 or 1 randomly on those cases. Then, they will exchange their basis with others, and they will find that in positions 2, 4 and 5, Bob used the wrong basis. So they will use the rest of the bit (1st, 3rd and 6th bit) string as the secret key—that is, 101. The rest is simple, just encrypt the message using that key and send it.
The situation becomes critical when Eve comes into action. As they are connecting using the public channel, it is quite possible that Eve will intercept the communication. In this case, as with the previous case, Alice encodes the bit information using any basis and sends it to Bob, but now Eve intercepts the qbits. Like Bob, Eve also has a decoder of the qbit. But Eve also doesn't know the basis Alice is using, so like Bob, she also randomly uses basis to decode the qbits. There is a 50% chance that Eve will use the right basis, and a 50% chance she will use the wrong basis. For the correct 50%, the photon's spin direction will not be affected, but for the wrong 50%, the photon's spin direction will be changed. For the 50% of qbits for which Eve used the right basis, Bob will use a 25% right basis and 25% wrong basis, and for the right 25% of qbits, he will get a 25% right qbit, and for the wrong 25% basis Bob used, he will get 12.5% of qbits correct just due to probability. That means from the first 50% for which Eve used the right basis, Bob will get 37.5% correct qbits. For the rest of the 50%, again Bob will use 25% right and 25% wrong basis. From this, Bob will get 12.5% and 12.5% due to probability, which means he will get 25% right qbits. So when Eve is between them, Bob will have 37.5 + 25 = 62.5% accuracy. Figure 6 demonstrates this calculation.
In Figure 6, the node with “**”, like C**, represents the nodes where Bob decoded the qbits correctly, and the node with “*”, like F*, represents the nodes where Bob decoded the qbits incorrectly. One question that may arise is why does Bob get 12.5% accuracy (in E,L) when he used the wrong basis? Remember that when you use a wrong basis to decode a qbit, there is a 50% chance that you will get a 0, and a 50% chance that you will get a 1. By this logic, Bob will have 12.5% accuracy from D. Similarly, in the case of I, when Bob has used the correct basis (with respect to Alice's basis) but Eve already has changed the polarization of the qbits using the wrong basis, Bob has a 50% chance of being right and a 50% chance of being wrong.
So overall, Bob gets 12.5% right qbits in I and 12.5% wrong qbits in J. Now they will match the basis they used for each qbit, and they will use the bits where Bob used the correct basis, and they will throw out the bits for which Bob used the wrong basis. Now they need to check whether Eve is listening. For that purpose, they will use a subset of the matched key (after throwing out the bits for which Bob used wrong basis) and compare with others using the normal channel. Bob will have 100% accuracy if Eve is not there; otherwise, Bob will have 75% accuracy in the basis comparison. If the accuracy is 100%, they will discard the set of bits they used for matching, and the rest of the bit string will be used as the key to encrypt the message. If 100% accuracy is not observed, they will try again to get a key using QKD.
In Table 2, Alice is sending a key of “01101011” to Bob using two types of polarization as stated above.
Table 2. Alice Sending a Key of 01101011 to Bob Using Two Types of Polarization
| Alice's basis | + | X | + | + | X | X | X | X |
| Alice's data | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| Eve's basis | + | + | X | + | X | X | X | + |
| Eve's data | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| Bob's basis | + | + | + | X | + | X | X | X |
| Bob's data | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Now Alice and Bob will compare their basis, and they will find that Bob has guessed the 1st, 3rd, 7th and 8th basis correctly. So they will throw out the bits for the remaining positions—that is, the 2nd, 4th, 5th and 6th. Now the key is “0011”. They will choose the first two bits for matching, and then they will find that their second bit in the key is different, which means Eve is between them. Then they will repeat the same procedure again until they get a 100% key match. When they get a key, they easily can encrypt the message using the key and send it via the public network.
In practice, the quantum channel also will be affected by noise, and it will be hard to distinguish between noise and eavesdropping.
If Eve wants, she can intercept the quantum channel just to not allow Alice and Bob to communicate.
No amplifiers are used on the optical fiber carrying the quantum signal. Such devices would disrupt the communication in the same way an eavesdropper does. This implies, in turn, that QKD's range is limited.
Following the no-cloning theorem, QKD can provide only a 1:1 connection. So the number of links will increase N(N – 1)/2, as N represents the number of nodes.
Researchers have been developing such systems for more than a decade. The DARPA Quantum Network, which became fully operational in BBN's laboratory in October 2003, has been continuously running in six nodes, operating through the telecommunications fiber between Harvard University, Boston University and BBN since June 2004. The DARPA Quantum Network is the world's first quantum cryptography network, and perhaps also the first QKD system providing continuous operation across a metropolitan area (arxiv.org/abs/quant-ph/0503058).
NIST performs core research on the creation, transmission, processing and measurement of optical qbits. It demonstrated high-speed QKD systems that generate secure keys for encryption and decryption of information using a one-time pad cipher, and extended them into a three-node quantum communications network (w3.antd.nist.gov/qin/index.shtml).
Toshiba's Quantum Key Distribution System delivers digital keys for cryptographic applications on fiber-optic-based computer networks based on quantum cryptography. In particular, it allows key distribution over standard telecom fiber links exceeding 100km in length and bit rates sufficient to generate 1 megabit per second of key material over a distance of 50km—sufficiently long for metropolitan coverage (https://www.toshiba-europe.com/research/crl/qig/quantumkeyserver.html).
The current status of quantum cryptography in Japan includes an inter-city QKD testbed based on DPS-QKD, a field test of a one-way BB84 system over 97km with noise-free WDM clock synchronization, and so on (“Toward New Generation Quantum Cryptography—Japanese Strategy” by Nukuikita, Koganei).
The 973 Program and 863 program of China have funded support to the QKD research (Post-Quantum Cryptography: Third International Workshop, Pqcrypto 2010, Darmstadt, Germany, May 25–28, 2010, Proceedings, 1st ed.).
In Europe, the SEcure COmmunication based on Quantum Cryptography (SECOQC, 2004–2008) project was funded for the same reason (http://vcq.quantum.at/publications/all-publications/details/643.html).
In 2004, ID Quantique was the first in the world to bring a quantum key distribution system to a commercial market. ID Quantique's QKD product was used in conjunction with layer 2 Ethernet encryption to secure elections in Geneva. Other companies, like MagicQ, QinetiQ and NEC, also are working in this field. Companies claim to offer or to be developing QKD products, but limited information is publicly available. However, it's likely that the situation will evolve in the near future (swissquantum.idquantique.com/?-Quantum-Cryptography-#).