
Genius is a calculator program that has both a command-line version and a GNOME GUI version. It should available in your distribution's package management system. For Debian-based distributions, the GUI version and the command-line version are two separate packages. Assuming that you want to install both, you can do so with the following command:
sudo apt-get install genius gnome-genius
If you use Ubuntu, be aware that the package gnome-genius doesn't appear to be in Bionic. It's in earlier versions (trusty, xenial and arty), and it appears to be in the next version (cosmic). I ran into this problem, and thought I'd mention it to save you some aggravation.
Starting the command-line version provides an interpreter that should be familiar to Python or R users.
Figure 1. When you start Genius, you get the version and some license information, and then you'll see the interpreter prompt.
If you start gnome-genius, you'll see a graphical interface that is likely to be more comfortable to new users. For the rest of this article, I'm using the GUI version in order to demonstrate some of the things you can do with Genius.
Figure 2. The GUI interface provides easy menu access to most of the functionality within Genius.
You can use Genius just as a general-purpose calculator, so you can do things like:
genius> 4+5
= 9
Along with basic math operators, you also can use trigonometric functions. This command gives the sine of 45 degrees:
genius> sin(45)
= 0.850903524534
These types of calculations can be of essentially arbitrary size. You also can use complex numbers out of the box. Many other standard mathematical functions are available as well, including items like logarithms, statistics, combinatorics and even calculus functions.
Along with functions, Genius also provides control structures like conditionals and looping structures. For example, the following code gives you a basic for loop that prints out the sine of the first 90 degrees:
for i = 1 to 90 do (
x = sin(i);
print(x)
)
As you can see, the syntax is almost C-like. At first blush, it looks like the semicolon is being used as a line-ending character, but it's actually a command separator. That's why there is a semicolon on the line with the sine function, but there is no semicolon on the line with the print function. This means you could write the for loop as the following:
for i = 1 to 90 do ( x = sin(i); print(x) )
Along with for loops, there are while loops, until loops, do-while loops, do-until loops and foreach loops. You also can control whether or not to pop out of a loop with the break and continue commands. They behave the same way that they do in languages like C. The conditional structure in Genius is a very basic if structure, so a basic if-then statement looks like the following:
if (a==5) then (a=a-1)
You also can use an else statement:
if (c>0) then (c=c-1) else (c=0)
Genius has no elseif statement.
You can use conditionals anywhere you would put an expression, which means you could use an if structure to set a variable value:
a = (if b>0 then b else 1)
As you can see, I didn't use parentheses here. You need to use them only in cases where the order of operations might be confusing.
So far, I've covered commands, variables, conditionals and looping structures. Genius also claims it uses a programming language called GEL. A programming language should have one last structure, the ability to organize code into reusable chunks. And, of course, GEL has the ability for end users to define their own functions. The basic syntax of a function definition looks like this:
function <identifier>(<comma separated arguments>) =
↪<function body>
As a really simple example, the following code defines a cubing function:
function my_cube(x) = x*x*x
You then can use it just like any other function:
genius> my_cube(3) = 27
Sometimes, you may need to be able to handle a variable list of input parameters to your function. In those cases, you define your function with the last parameter being "...". It looks like the following:
function my_func(a, b, c...) = <function body>
In such cases, the input parameters are handed to your function body as a vector of values.
When you start writing larger pieces of code, you likely will need to start handling error conditions. Genius (and, hence, GEL) has basic error handling capabilities. When you detect an error in your code, you can send a message to the end user with the error command:
if not IsMatrix (M) then (
error("M is not a matrix")
)
This might not be enough, however. If the error isn't recoverable, you'll need to stop execution somehow. GEL provides two options. The first is to stop the current function and go back to the calling code using the bailout command. If the error is extremely horrendous, you may need to stop all execution. In those cases, you can use the exception command.
Genius also has a huge number of advanced functions. As an example of the kinds of advanced calculations you can do, let's look at doing a numerical integration. You can integrate a function, from a start limit to an end limit. For example, you can find the numerical integral of the sine function from 0 degrees to 180 degrees with the following:
genius> NumericalIntegral(sin, 0, 180) = 1.59846942736
You also can do infinite sums, numerical derivatives and limits.
The last item I want to look at is available only with the GNOME version of Genius. In this case, you have the ability to plot data and functions and display them on the screen. When you click on the plot button on the main window, you'll get a new window where you can define the plot parameters.
Figure 3. The "Create Plot" window lets you define both line plots and surface plots for multiple functions.
Since you can plot multiple functions, you can see them side by side in the same window. If, instead, you need to do a 3D plot of a surface, you can select the surface plot tab of the plotting window and define a function in terms of x and y. Within the plot window, there are several options for changing the view. For the surface plot, you even can make it rotate so you can see the resultant plot from all angles. When you have the plot looking exactly the way you want, click the Graph menu entry and export it to one of several file formats so you can use it in other publications or reports.
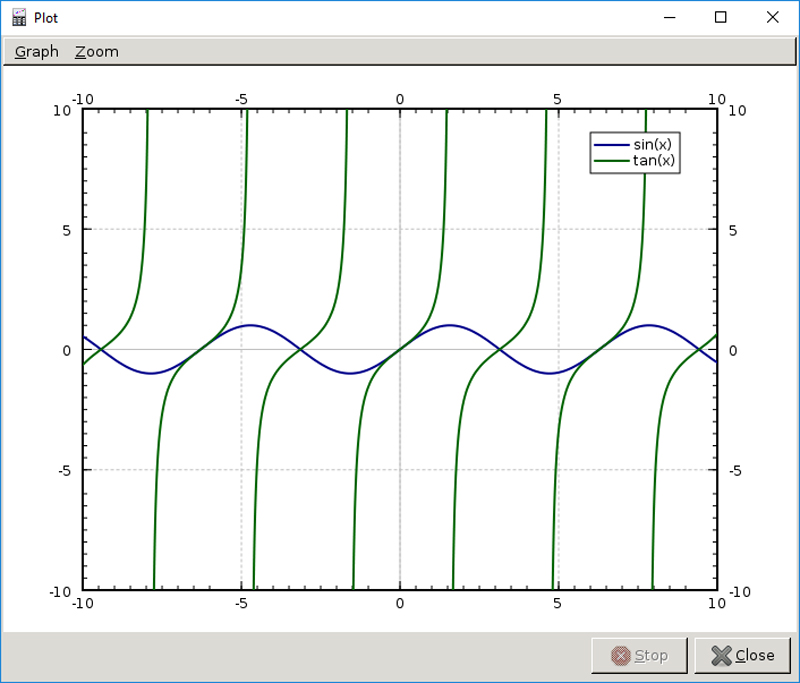
Figure 4. GNOME Genius lets you plot multiple functions easily. For example, you could plot sine and tangent in order to see how they compare to each other.
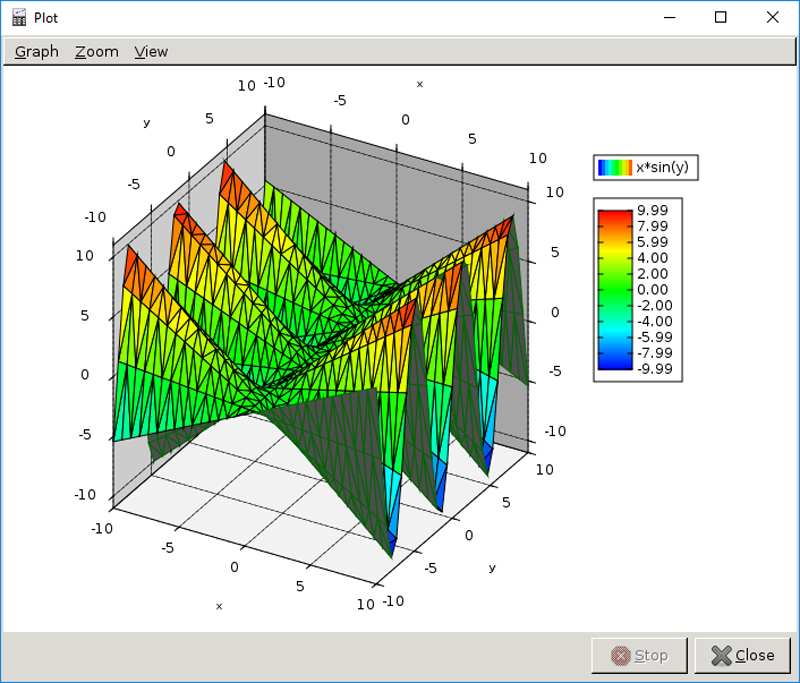
Figure 5. You easily can plot a single function in terms of x and y—for example, x*sin(y).
As you can see, Genius provides a fair bit of functionality within a small package. It's been used in education to allow students to see the results of different calculations quickly and to show how they vary based on inputs or changes in algorithm. As well, it provides the essentials of an advanced scientific calculator. People who have used the HP or TI advanced hand-held calculators will find Genius a very powerful replacement on the desktop. You can find much more information at the main website, including the manual and a set of examples.
—Joey Bernard